
Zadanie Prostokąt arytmetyczny (ari)
Pomóż nam usprawnić bazę zadań!
Prostokąt arytmetyczny
Limit pamięci: 256 MB
Po lekcji o ciągach arytmetycznych nauczyciel dał Piotrusiowi zadanie domowe:
kartkę papieru z kratownicą o wymiarach 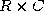 , której niektóre pola były wypełnione liczbami.
Pewna liczba pól była pusta (potencjalnie zero).
Zadaniem Piotrusia jest utworzenie prostokąta arytmetycznego poprzez wypełnienie
pustych pól liczbami.
W prostokącie arytmetycznym liczby w każdym wierszu i w każdej kolumnie tworzą ciąg arytmetyczny w kolejności występowania w tym wierszu/kolumnie.
, której niektóre pola były wypełnione liczbami.
Pewna liczba pól była pusta (potencjalnie zero).
Zadaniem Piotrusia jest utworzenie prostokąta arytmetycznego poprzez wypełnienie
pustych pól liczbami.
W prostokącie arytmetycznym liczby w każdym wierszu i w każdej kolumnie tworzą ciąg arytmetyczny w kolejności występowania w tym wierszu/kolumnie.
Dla przykładu, to jest prostokąt arytmetyczny rozmiaru 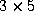 :
:
| 1 | 3 | 5 | 7 | 9 |
| 2 | 2 | 2 | 2 | 2 |
| 3 | 1 | -1 | -3 | -5 |
Piotruś jest zbyt leniwy, by rozwiązywać takie zadania ręcznie. Chciałby mieć program, który zrobi to za niego.
Zadanie
Masz dany prostokąt wypełniony liczbami całkowitymi oraz kropkami. Sprawdź, czy jest możliwe zastąpienie kropek pewnymi liczbami wymiernymi, tak aby otrzymać prostokąt arytmetyczny. Jeśli istnieje rozwiązanie, wypisz jedno z nich.
Uwaga: Ciągiem arytmetycznym nazywamy taki ciąg liczb, w którym różnica pomiędzy każdymi dwoma kolejnymi elementami jest stała.
Specyfikacja wejścia
Pierwszy wiersz wejścia zawiera jedną liczbę całkowitą 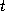 (
(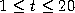 ): liczbę przypadków testowych do rozważenia.
W kolejnych wierszach następuje opis poszczególnych przypadków testowych.
): liczbę przypadków testowych do rozważenia.
W kolejnych wierszach następuje opis poszczególnych przypadków testowych.
Pierwszy wiersz opisu zawiera dwie liczby całkowite dodatnie 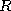 oraz
oraz 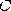 : wymiary prostokąta.
Potem następuje
: wymiary prostokąta.
Potem następuje 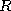 wierszy, z których każdy zawiera
wierszy, z których każdy zawiera 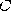 elementów pooddzielanych pojedynczymi odstępami.
Każdy z tych elementów jest albo kropką (.), albo liczbą całkowitą.
elementów pooddzielanych pojedynczymi odstępami.
Każdy z tych elementów jest albo kropką (.), albo liczbą całkowitą.
Ograniczenia
Każda z liczb wpisanych już do prostokąta jest między -100 a 100, włącznie.
Testy dzielą się na 10 grup, z których każda warta jest 10 punktów.
W grupach od 1 do 9 zachodzi 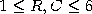 .
Własności poszczególnych grup podane są poniżej.
.
Własności poszczególnych grup podane są poniżej.
Grupa 1. Kratownica jest całkowicie wypełniona liczbami.
Grupa 2. W każdym teście 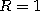 lub
lub 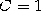 .
.
Grupa 3. W każdym teście 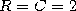 .
.
Grupa 4. Każdy test ma dokładnie jedno rozwiązanie, które można znaleźć za pomocą metody opisanej w pierwszym przykładzie (poniżej).
Grupa 5. Każdy test ma dokładnie jedno rozwiązanie, które na dodatek składa się tylko z liczb całkowitych.
Grupa 6. Każdy test ma dokładnie jedno rozwiązanie.
Grupa 7. Każdy test ma dokładnie jedno rozwiązanie, które składa się tylko z liczb całkowitych, albo nie ma rozwiązania w ogóle.
Grupa 8. Każdy test ma dokładnie jedno rozwiązanie albo nie ma rozwiązania w ogóle.
Grupa 9. Dowolne testy.
Grupa 10. Dowolne testy, w których 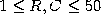 .
.
Specyfikacja wyjścia
Twój program powinien wypisać kolejno wyniki dla wszystkich przypadków testowych, w następującym formacie.
Jeśli nie ma rozwiązania, wypisz jeden wiersz z napisem "No solution." (bez cudzysłowów). Jeśli jest wiele rozwiązań, wybierz jedno z nich.
Wypisując rozwiązanie dla danego przypadku testowego, umieść
na wyjściu  wierszy, każdy zawierający
wierszy, każdy zawierający  liczb wymiernych pooddzielanych pojedynczymi odstępami.
liczb wymiernych pooddzielanych pojedynczymi odstępami.
Każdą liczbę wymierną należy wypisać w formacie "N/D", przy czym D jest dodatnie, a N i D są względnie pierwsze. Jeśli D jest równe 1, pomiń część "/D".
Żadna z liczb na wyjściu nie może mieć więcej niż 20 cyfr. (Spełnienie tego wymagania nie powinno być trudne, jego jedynym celem jest ułatwienie sprawdzania odpowiedzi).
Przykłady
Dla danych wejściowych:
1 3 5 . . 3 . 5 . . . 5 . . . . . 7
poprawną odpowiedzią jest:
1 2 3 4 5 2 3 4 5 6 3 4 5 6 7
Powyższy przykład można rozwiązać następująco: najpierw zauważ, że drugą liczbą w ostatniej kolumnie musi być 6. Potem wypełnij pierwszy wiersz, drugi wiersz, a na koniec kolumny od pierwszej do czwartej.
Dla danych wejściowych:
1 1 6 4 . . 0 . .
poprawną odpowiedzią jest:
4 8/3 4/3 0 -4/3 -8/3
Dla danych wejściowych:
1 1 4 1 2 . 2
poprawną odpowiedzią jest:
No solution.
Dla danych wejściowych:
1 3 3 1 . . . 2 . . . 3
poprawną odpowiedzią jest:
1 0 -1 3 2 1 5 4 3
To jest jedno z wielu możliwych rozwiązań dla tych danych wejściowych.
Autor zadania: Michal Forisek.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English